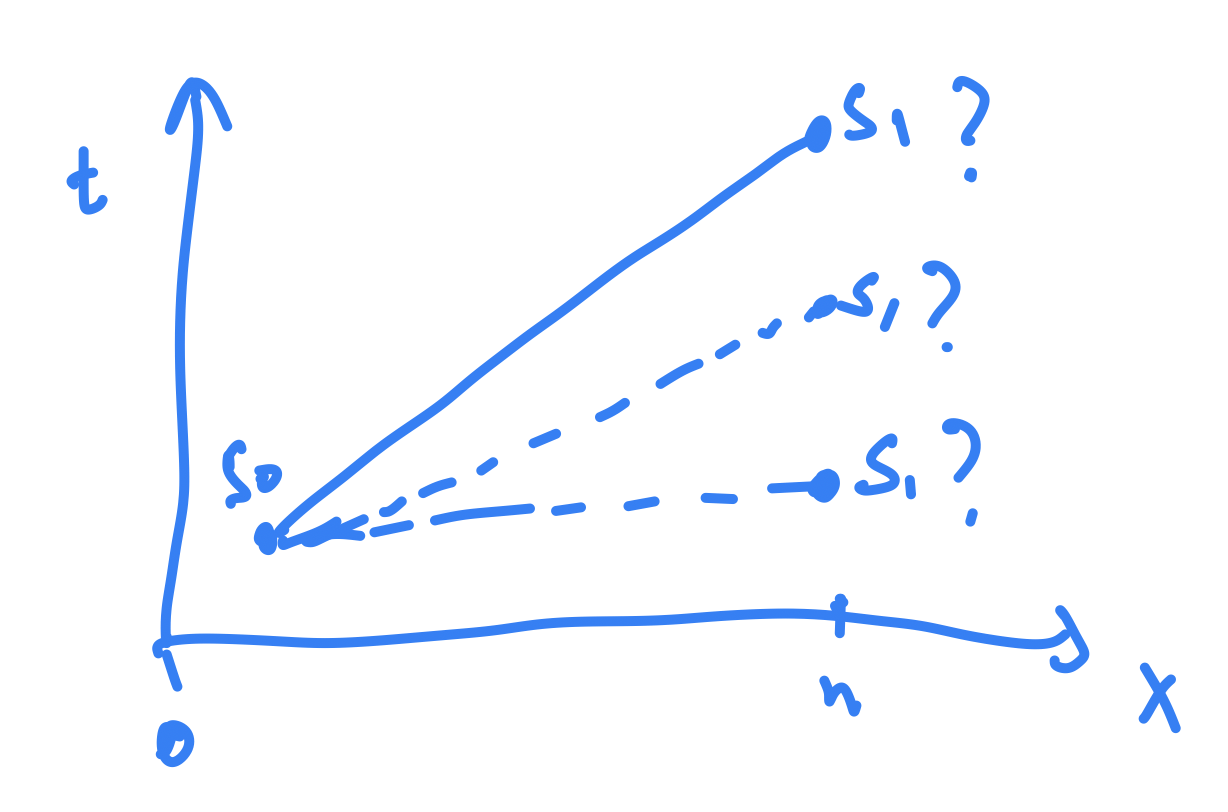
Setup here

An agents path through time and space is represented by the curve from $s_0$ to $s_1$. I’m trying to use calculus of variations to find a space-time rod (curve) that minimizes the kinetic energy of the agent $\frac{1}{2}mv^2$.

Here, $t$, time, is represented by the $y$-axis, and $x$, position, is on the $x$-axis. The rod’s start point is $s_0$ and end point is $s_1$. Generalized coordinates are $q(s) = [x\;t] (s)$

Euler Lagrange with slightly different B.C

Start with the Euler Lagrange equations:

\[\frac{d}{ds}\frac{\partial L}{\partial \dot{q}} = \frac{\partial L}{\partial q}\]

The Calc of Var derivation for the E.L. equations includes the boundary conditions that there is no variation at $s_0$ and $s_1$ (so $q(s_0)$ is known and $q(s_1)$ is known). However, in our problem, $q(s_1)$ is unknown, so $t(s_1)$ is unknown, which leads to another boundary condition that at $s_1$:

\[\frac{\partial L(s_1)}{\partial \dot{q}} = 0\]

Least Action minimization

Let $L(s) = T(s) = \frac{1}{2}mv^2$. Over the domain of the rod, the principle of least action can be written as:

\[S = \int_s Tds = \int_s \frac{1}{2}m(\frac{\partial x}{\partial s}(\frac{\partial t}{\partial s})^{-1})^T (\frac{\partial x}{\partial s}(\frac{\partial t}{\partial s})^{-1})\]

Simplified notation \(S = \int_s \frac{1}{2}m(\dot{x}\dot{t}^{-1})^2\)

Minimize the action using the E.L. equations

\[\frac{d}{ds}\frac{\partial T}{\partial \dot{q}} = \frac{\partial T}{\partial q}\]

Since $T$ doesn’t depend on $q$.

\[\frac{d}{ds}\frac{\partial T}{\partial \dot{q}} = \frac{\partial T}{\partial q} = 0\]

Vectorized notation

\[\frac{d}{ds}\frac{\partial T}{\partial [\dot{x}\;\dot{t}]} = \frac{d}{ds}[\frac{\partial T}{\partial \dot{x}} \; \frac{\partial T}{\partial \dot{t}}] = 0\] \[[\frac{\partial T}{\partial \dot{x}} \; \frac{\partial T}{\partial \dot{t}}] = [2m\dot{x}\dot{t}^{-2} \; -2m\dot{x}^2\dot{t}^{-3}]\]

After using the product rule and chain rules:

\[\frac{d}{ds}[\frac{\partial T}{\partial \dot{x}} \; \frac{\partial T}{\partial \dot{t}}] = [(2m\ddot{x}\dot{t}^{-2} - 4m\dot{x}\dot{t}^{-3}\ddot{t}) \; (-4m\dot{x}\dot{t}^{-3}\ddot{x} + 6m\dot{x}^2 \dot{t}^{-4} \ddot{t})] = 0\]

with b.c. $q(s_0) = [x_0 \; t_0]$ and $\frac{\partial L(s_1)}{\partial \dot{q}} = 0$.

Thats the differential equation. I think… Its a bit ridiculous.