Yale Financial Markets Lecture 2

Model

• Exogenous variables $e$ (incontrollable variables)
• Endogenou variables $x$ (prices, consumption, predictable variables)
• Equilibrium conditions $F(e,x) = 0$
• Equilibrium $x(e)$ s.t. $F(e, x(e)) = 0$
• Comparative Statics -> what happens when you change $e$.

Why models?

• Prediction, understanding
• Properties of equil

Ricardo: first economic model- principle of comparative advantage. Malthus: Models are based on assumptions, which propagate errors

Market Mechanisms

• Seller determined prices
• Haggling
• Govt price regulation
• Paris Bourse - tatonnement
• Commodities futures pit
• Bid/Ask prices

NYSE Beginnings

• Founded in 1792 by 24 brokers on wall stree
• Only 5 securities traded. 3 war bonds, 2 bank stocks
• Sold in a double auction format

Walrus 1871

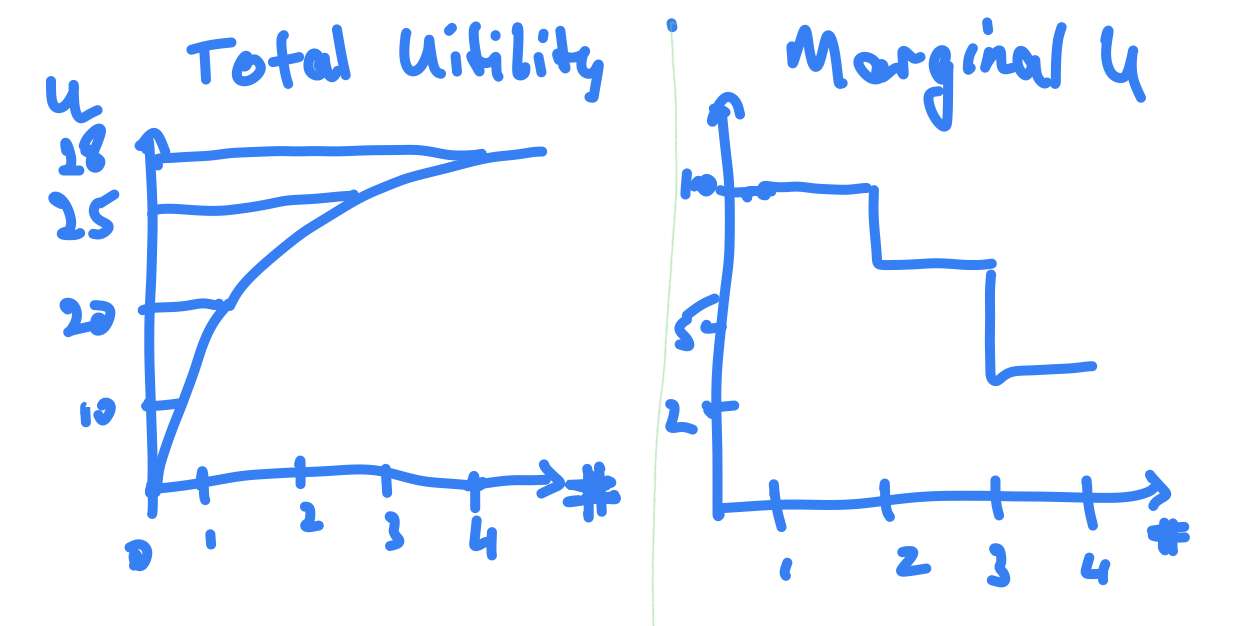
• Marginal utility
• Utility increases with more stuff but at smaller and smaller rate.

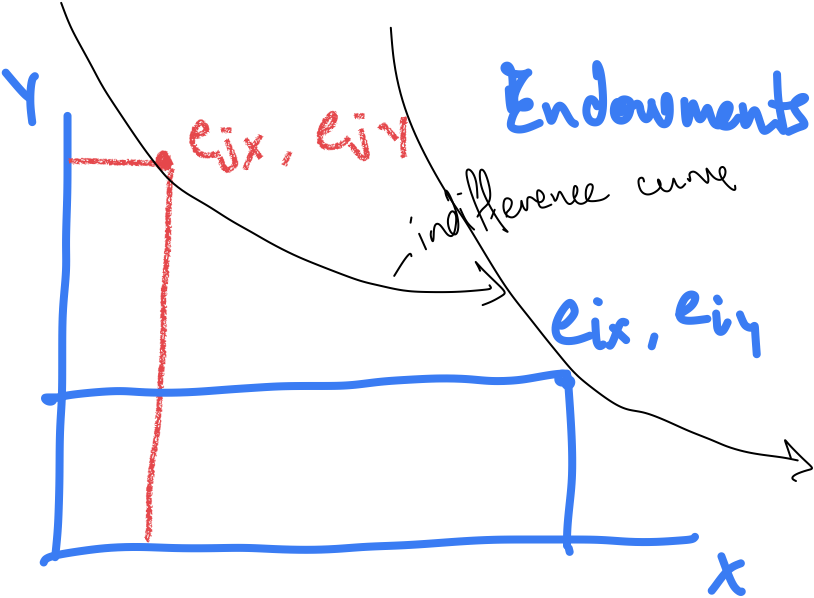
Endowments (what do I have?)

• $x$ is money
• $y$ is goods

General Equilibrium Model

Exogenous Variables

• Individual $i \epsilon I$ where each $i$ has a utility and an endowment
  • Welfare $W_i(x, y) = u_i(x) + v_i (y)$
    • $y$ is money
    • $x$ is football tickers
  • Endowment $e_i = (e_{ix}, e_{iy})$

Endogenous Variables

• Prices $(P_x, P_y)$
• Trades, or final consumptions $(x, y)$

Equilibrium

\[F(e, x) = 0\]

Budget set of agent $i$ is the linear trade-off between $x, y$ defined by:

\[P_x(x^i - e_{ix}) + P_y(e_{iy} - y^i) = 0\]

Final consumption must equal final endowment.

General Equilibrium for 2 agents:

1. $\sum_i x_i = \sum_i e_{ix}
2. $\sum_i y_i = \sum_i e_{iy}
3. $P_x(x^i - e_{ix}) + P_y(e_{iy} - y^i) = 0$
4. $P_x(x^j - e_{jx}) + P_y(e_{jy} - y^j) = 0$
5. $\frac{MarginalUtility_i(x)}{MarginalUtility_i(y)} = \frac{P_x}{P_y}$
6. $\frac{MarginalUtility_j(x)}{MarginalUtility_j(y)} = \frac{P_x}{P_y}$